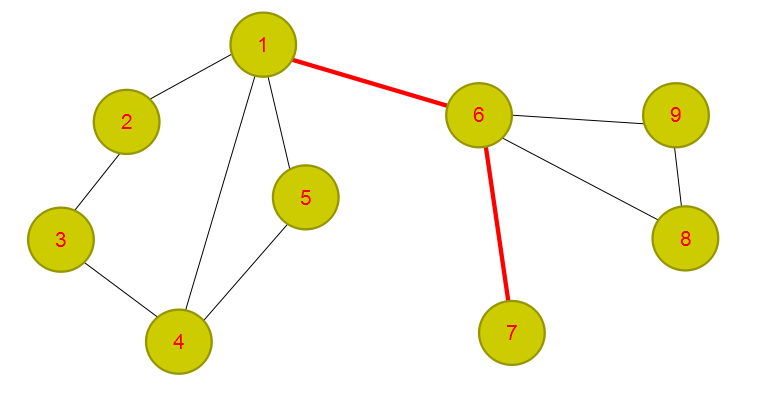
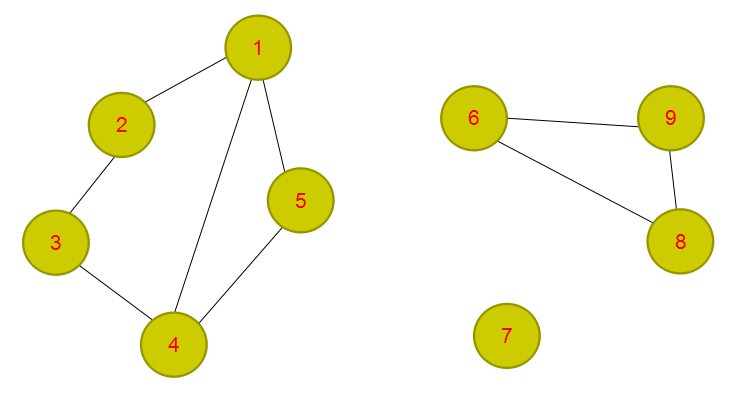
从外地学习回来，我对图论才有认识（以前就没接触过，非常尴尬），说实话，学好图论的重要性，就像学数学时在进行解析几何时，图极有可能是打开答案的最后秘钥，也就是数形结合，而懂的人永远明白，用图解决绝对比用解析简单（一般情况）。而图论对于oi选手说，就是一大杀器，有可能利己，也可能抱憾终身。所以说图论的重要性就很显然了。

上一次我们讲到了边双，这次我们来看点双。

说实话来说，点双比边双稍微复杂一些；

学完边双，我们先看一道题

第一问都不用说了吧，多余的道路，明显的割边。

是不是首先想到用边双，但是我们来看一个图：

**

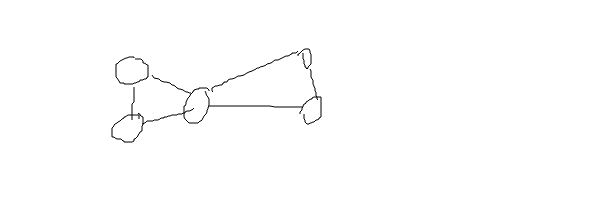有点丑，但是凑活看吧。

它是一个边双，但是！！！！它竟然没有冲突的边！！！

此时我们就要用点双了（是不是想打死我，竟然没讲，先坑人）

前言

本来应该先说强连通分量，但是有一定的分配，所以这个在下一篇博客将会见到。

这个本想连点连通分量一起讲，但是量有点大，所以我就分两步讲。

边双

定义

核心概念:没有割边;

割边只会把图分成两部分对图中的点没有影响;

再来看看图解

很容易就能发现，只要将割边断掉，然后剩下的连通块就是我们的边双，那么我们的代码就可以yy出来了，先跑一遍Tarjan求割点，然后在去跑dfs，将每一个边双染色，那么就可以了,而染色操作，以便于我们后面好缩点。

所谓割点（顶）割边，我们引进一个概念

割点：删掉它之后(删掉所有跟它相连的边)，图必然会分裂成两个或两个以上的子图。
割边(桥)：删掉一条边后，图必然会分裂成两个或两个以上的子图，又称桥。

这样大家就应该能简单理解（怎么可能）割点割边了。

所以我们再来看一个图

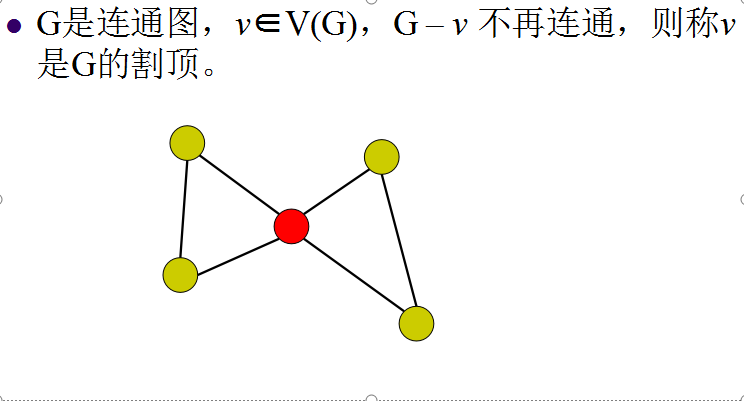
这样大家就能明白了吧（明白是明白了，但是要他干嘛（自动忽略））到后面会明白的。

前言

​ 这个本来应该在从外地学习回来之后就因该写的,但是只写了一半,不过看看自己以前写的,果然还是理解太浅了;

正文

也许有很多人觉得最短路就是那几个算法，不过也确实，但是我们的难点主要在建图上。

但是既然是基础，那么就应该好好掌握做法，多敲几遍就好了。

最短路主要的几个算法有 $\text{Dijkstra,floyd,Bellman-ford}$ 和$\text{SPFA}$，而SPFA是Bellman-ford的队列优化，所以一般用SPFA算法。