关于KMP

​ KMP其实是三个人名字的缩写,因为是他们同时发现的(大佬惹不起);

​ KMP作为CSP考点,主要亮点是其优秀的匹配复杂度,而且消耗空间小,比起hash虽然有些局限性,但是因为其正确率高,所以经常被人使用.

前置知识

​ 关于字符串的读取,以及字符串相关操作的基础了解,这里涉及字符串匹配以及子串;

预备知识

​ 说实话,基环树一般比较综合,所以一般只要就要具有图论基本知识便可以开始学习.

警告

​ 博主实力不足,如果出错,请用力D他 .

认识

​ 基环树,原体是树,有树上任意连一条边,就成了一个环,即基环树,一般特征,$n$个点$n$条边;

​ 由于有树的特征,所以经常会用一些树的算法来计算基环树;

　　差分，也就是数与数之间的差值。拿一维差分来举例子，将差分设为c[ ]数组，原数为a[ ],那么

　　$c[i]=a[i]-a[i-1]$

　　这便是简单的差分数组；

　　那么要他何用？

　　最为主要的作用就是区间的修改，那么在修改之前，我们先明白如何将原数求出。很显然，$c[1]$~$c[i]$差分数组求和即可得到$a[i]$。

请在学习之前有一定的线段树基础

在一些题中，它总会给你一些矩形，之后让你求总覆盖面积。

它的难点在于，有重叠面积，如果只是罗列情况，那么只会一事无成。

所以说，这里就引进了扫描线做法；

其实它的原理很简单，只是底*高而已，只是分段求解；

而问题大概的图就是这样

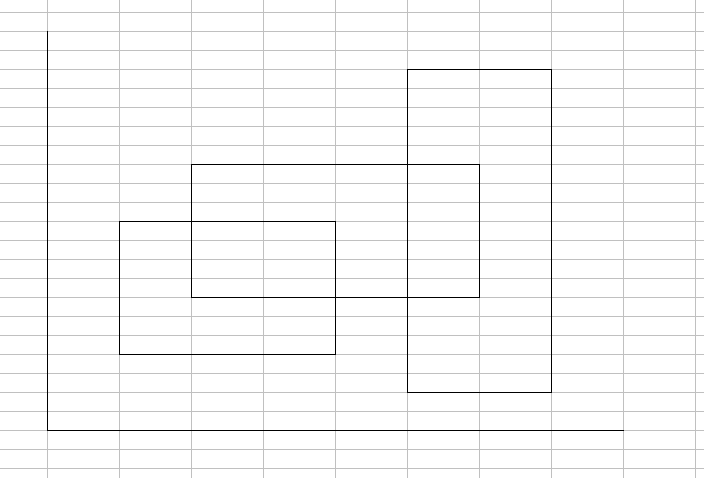
根据我刚刚说的分段求解和底*高，那么我们就可以推测出扫描线是什么了

例题 P1169 [ZJOI2007]棋盘制作

题目描述

国际象棋是世界上最古老的博弈游戏之一，和中国的围棋、象棋以及日本的将棋同享盛名。据说国际象棋起源于易经的思想，棋盘是一个8×88 \times 88×8大小的黑白相间的方阵，对应八八六十四卦，黑白对应阴阳。

而我们的主人公小Q，正是国际象棋的狂热爱好者。作为一个顶尖高手，他已不满足于普通的棋盘与规则，于是他跟他的好朋友小W决定将棋盘扩大以适应他们的新规则。

。。。。

有点懒；

需要先理解几个概念：

1. LCA

2. 线段树（熟练，要不代码能调一天）

3. 图论的基本知识（dfs序的性质）

这大概就好了；

定义：

　　1.重儿子：一个点所连点树size最大的，这个son被称为这个点的重儿子；

　　2.轻儿子：一个点所连点除重儿子以外的都是轻儿子；

　　3.重链：从一个轻儿子或根节点开始沿重儿子走所成的链；

莫队思想浅谈

莫队，基于分块思想。

所以说，在学习莫队时可以先了解一下分块的优化原理，这对于莫队的理解会有帮助；

我们将分层次讲解，难度不断增加，并附有例题。。。（由于博主太烂懒，所以莫队的模板概念知识只会在这里叙述）

1.莫队：

　　基础的莫队是用来解决区间离线查询问题，利用分块原理和排序，将查询时的重叠部分集中以来优化的算法，大多的算法的复杂度为$O(nsqrt(n))$，实际更优；

Gauss算法，称为高斯消元算法，用来解决n元一次方程，在解决线性方程问题起着重要作用。

简述

　　运用高斯消元的方法，我们可以在O(n3)的时间求出n元线性方程，但是由于时间复杂度的原因，请注意题目数据范围的提示。

　　高斯消元三大定理（在小学就学过了吧）：

　　　　1.两个方程互换位置，解不变；

　　　　2.一个方程进行加减乘除，解不变；

manacher算法的由来不再赘述，自行百度QWQ。。。

进入正题，manacher算法是一个高效的计算回文串的算法，回文串如果不知道可以给出一个例子：“ noon ”，这样应该就很清晰了；

其实这个算法虽然名字长，但是实际代码很短，而且理解起来并不难。。。（连我这种蒟蒻都懂了）

这里给出模板题

题目描述

给出一个只由小写英文字符a,b,c…y,z组成的字符串S,求S中最长回文串的长度.

先存代码

AC自动机（简单版）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49

#include<bits/stdc++.h>
#define maxn 1000007
using namespace std;
int n,ans;
int tr[maxn][28],val[maxn],cnt,fail[maxn];
char mod[maxn],tx[maxn];
queue<int >q;

void build(char *a){
    int now=0;
    for(int i=0;a[i];i++){
        if(!tr[now][a[i]-'a']) tr[now][a[i]-'a']=++cnt;
        now=tr[now][a[i]-'a'];
    }
    val[now]++;
}//建树 

void AC(){
    for(int i=0;i<26;i++) if(tr[0][i]) q.push(tr[0][i]);//26个字母跑 
    while(!q.empty()){
        int u=q.front();q.pop();
        for(int i=0;i<26;i++){
            if(tr[u][i]) fail[tr[u][i]]=tr[fail[u]][i],q.push(tr[u][i]);//调取指针 
            else tr[u][i]=tr[fail[u]][i];//建立“虚边”——指向失配指针的i边
            //这里已经改变了trie图 
        }
    }
}

int query(char *t){
    int ol=0,u=0;
    for(int i=0;t[i];i++){
        u=tr[u][t[i]-'a'];
        for(int j=u;j&&val[j]!=-1;j=fail[j])
            ol+=val[j],val[j]=-1;//fail跳（这样其实很慢） 
    }
    return ol;
}

int main(){
//    freopen("cin.in","r",stdin);
//    freopen("co.out","w",stdout);
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
        scanf("%s",mod),build(mod);
    AC();
    scanf("%s",tx);ans=query(tx);
    printf("%d\n",ans);
}