A Huster

0%

Tarjan初步-强联通分量

Posted on Valine:

前言

​ 发现我又咕咕了一篇早就应该写的博客,唉,真是的;

​ 强联通分量常用于缩点,重建图去跑其他算法;

入门

​ 强联通分量存在于有向图,简单的概念即有向图中一个块中的点可以彼此到达,这个块被称为分量,而两点彼此能到到达称为强联通,那么强联通分量的概念就出来了;

​ 同样用的时间戳(dfn)与返祖标记(low)这个概念,如果不知道,请看本博客中的点双边双;

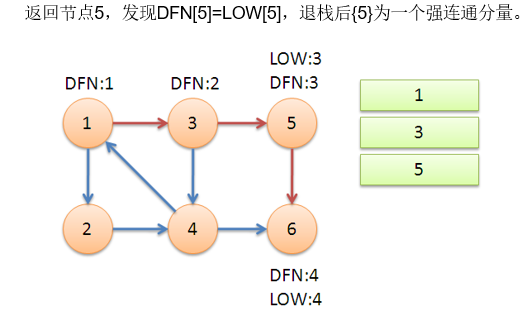
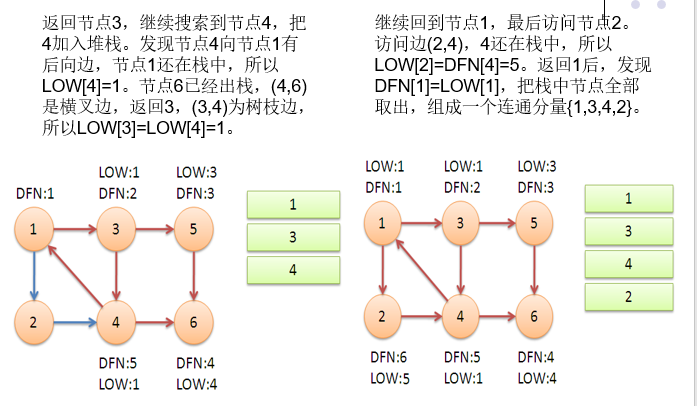
​ 与点双相同的是当一个点dfn=low时,那么其栈中的点到这个点,即这个搜索子树就是就是一个强联通分量;

模拟

​ 有一定基础,或者已经理解了话可以跳过该过程,这里不再给出严谨证明;

altSUJ[B`RCUTE.png)

alt

alt

例题1

​ P2341 [HAOI2006]受欢迎的牛

模版题;

每头奶牛都梦想成为牛棚里的明星。被所有奶牛喜欢的奶牛就是一头明星奶牛。所有奶

牛都是自恋狂，每头奶牛总是喜欢自己的。奶牛之间的“喜欢”是可以传递的——如果A喜

欢B，B喜欢C，那么A也喜欢C。牛栏里共有N 头奶牛，给定一些奶牛之间的爱慕关系，请你

算出有多少头奶牛可以当明星。

​ 如果没有环,那么就是一个没有出度的点,如果有强联通分量,那么只要统计每个强联通分量的出度即可;

​ 答案就是那个出度为0强联通分量中点的个数,记住特判一下有多个出度为0的强联通分量,这样答案会是0;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include<bits/stdc++.h>
#define d 10000
using namespace std;
int n,m,head[20007],cent,low[20007],dfn[20007],t,stackk[20007];
int top,temp,col[20007],vis[20007],cnt;
int out[10007],tot[10007],fu[10007];
struct node{
	int next,to;
}edge[100007];

void add(int u,int v){
	edge[++cent]=(node){head[u],v};head[u]=cent;
}

void Tarjan(int x){
	low[x]=dfn[x]=++t;vis[x]=1;
	stackk[++top]=x;
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(!dfn[y]){
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}else if(vis[y]){
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(dfn[x]==low[x]){
		cnt++;
		do{
			temp=stackk[top--];
			vis[temp]=0;
			col[temp]=cnt;
			tot[cnt]++;
		}while(temp!=x);//注意特判条件
	}
}

int main(){
	scanf("%d%d",&n,&m);
	for(int i=1,a,b;i<=m;i++){
		scanf("%d%d",&a,&b);
		add(a,b);
	}
	for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i);
	for(int i=1;i<=n;i++){
		for(int j=head[i];j;j=edge[j].next){
			int y=edge[j].to;
			if(col[y]!=col[i]){
				fu[col[i]]++;//统计出度
			}
		}
	}
	int flag=0;
	for(int i=1;i<=cnt;i++){
		if(!fu[i]){
			if(flag){printf("0");return 0;}
			flag=i;
		}
	}
	printf("%d",tot[flag]);
}

例题2

​ P2746 校园网

求一个有向图入度为0的点的个数,和连多少条边能使图互相连通;

​ 我怎么又放了一道模版题

​ 缩点一下,求出入度为0的点即可,下一问,我们可以将入度为0的点和出度为0的点两两配对,如果不够,将多出来的随便接在一个上面即可(因为已经匹配完的是一个强联通分量)

code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include<bits/stdc++.h>
using namespace std;
int n,head[1007],cent,dfn[1007],low[1007],t,cnt;
int stackk[1007],top,col[1007],tot[1007],vis[1007];
int ans1,ans2,out[1007],in[1007];
struct node{
	int next,to;
}edge[10000007];
int min(int a,int b){return a<b?a:b;}

void add(int u,int v){
	edge[++cent]=(node){head[u],v};head[u]=cent;
}

void Tarjan(int x){
	dfn[x]=low[x]=++t;vis[x]=1;
	stackk[++top]=x;
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(!dfn[y]){
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}else if(vis[y]){
			low[x]=min(low[x],dfn[y]);
		}
	}
	if(dfn[x]==low[x]){
		cnt++;int z;
		do{
			z=stackk[top--];
			col[z]=cnt;
			vis[z]=0;
			tot[cnt]++;
		}while(z!=x);
	}
}

int main(){
	scanf("%d",&n);
	for(int i=1,s;i<=n;i++){
		scanf("%d",&s);
		while(s) add(i,s),scanf("%d",&s);
	}
	for(int i=1;i<=n;i++){
		if(!dfn[i]) Tarjan(i);
	}
	for(int x=1;x<=n;x++){
		for(int i=head[x];i;i=edge[i].next){
			int y=edge[i].to;
			if(col[y]==col[x]) continue;
			out[col[x]]++;in[col[y]]++;
		}
	}
	for(int i=1;i<=cnt;i++){
		if(!out[i]) ans2++;
		if(!in[i]) ans1++;
	}
	if(cnt==1) printf("1\n0");
	else printf("%d\n%d",ans1,max(ans1,ans2));
}

例题3

P3627 抢掠计划

Siruseri 城中的道路都是单向的。不同的道路由路口连接。按照法律的规定， 在每个路口都设立了一个 Siruseri 银行的 ATM 取款机。令人奇怪的是，Siruseri 的酒吧也都设在路口，虽然并不是每个路口都设有酒吧。

Banditji 计划实施 Siruseri 有史以来最惊天动地的 ATM 抢劫。他将从市中心 出发，沿着单向道路行驶，抢劫所有他途径的 ATM 机，最终他将在一个酒吧庆 祝他的胜利。

使用高超的黑客技术，他获知了每个 ATM 机中可以掠取的现金数额。他希 望你帮助他计算从市中心出发最后到达某个酒吧时最多能抢劫的现金总数。他可 以经过同一路口或道路任意多次。但只要他抢劫过某个 ATM 机后，该 ATM 机 里面就不会再有钱了。

​ Tarjan+SPFA(Dij);

​ 我们可以发现题目中给了我们提示;

他可以经过同一路口或道路任意多次;

​ 那么就是强联通分量缩点,一个强联通分量中的钱是可以全部拿走的,直接在缩点的图SPFA就行了;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include<bits/stdc++.h>
#define maxn 500007
using namespace std;
int n,m,head[maxn],dfn[maxn],low[maxn],val[maxn],stk[maxn],col[maxn];
int vis[maxn],cent,a[maxn],s,op[maxn],tot,cnt,top,p,dis[maxn],ans;
struct node{
	int next,from,to;
}edge[maxn<<2];

template<typename type_of_scan>
inline void scan(type_of_scan &x){
	type_of_scan f=1;x=0;char s=getchar();
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
	while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
	x*=f;
} 
template<typename top,typename... tops>
inline void scan(top &x,tops&... X){
	scan(x),scan(X...);
}

inline void add(int u,int v){
	edge[++cent]=(node){head[u],u,v};head[u]=cent;
}

void Tarjan(int x){
	dfn[x]=low[x]=++tot;vis[x]=1;
	stk[++top]=x;
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(!dfn[y]){
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}else if(vis[y]) low[x]=min(low[x],dfn[y]);
	}
	if(dfn[x]==low[x]){
		cnt++;int temp;
		do{
			temp=stk[top--];
			vis[temp]=0;
			col[temp]=cnt;
			val[cnt]+=a[temp];
		}while(temp!=x);
	}
}

queue<int>q;
void spfa(int s){
	dis[s]=val[s];vis[s]=1;q.push(s);
	while(!q.empty()){
		int x=q.front();q.pop();vis[x]=0;
		for(int i=head[x];i;i=edge[i].next){
			int y=edge[i].to;
			if(dis[y]<dis[x]+val[y]){
				dis[y]=dis[x]+val[y];
				if(!vis[y]) q.push(y),vis[y]=1;
			}
		}
	}
}

int main(){
//	freopen("cin.in","r",stdin);
	scan(n,m);
	for(int i=1,u,v;i<=m;i++) scan(u,v),add(u,v);
	for(int i=1;i<=n;i++) scan(a[i]);
	for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i);
	int lim=cent;cent=0;
	memset(head,0,sizeof head);
	for(int i=1;i<=lim;i++){
		int x=edge[i].from,y=edge[i].to;
		if(col[x]!=col[y]) add(col[x],col[y]);
	}
	scan(s,p);dis[col[s]]=val[col[s]];
	spfa(col[s]);
	for(int i=1;i<=p;i++) scan(op[i]),ans=max(ans,dis[col[op[i]]]);
	printf("%d\n",ans);
}

例题4

​ P3119 草鉴定

约翰有n块草场，编号1到n，这些草场由若干条单行道相连。奶牛贝西是美味牧草的鉴赏家，她想到达尽可能多的草场去品尝牧草。

贝西总是从1号草场出发，最后回到1号草场。她想经过尽可能多的草场，贝西在通一个草场只吃一次草，所以一个草场可以经过多次。因为草场是单行道连接，这给贝西的品鉴工作带来了很大的不便，贝西想偷偷逆向行走一次，但最多只能有一次逆行。问，贝西最多能吃到多少个草场的牧草。

​ 显然一个强联通分量中的点可以互相到达,缩点即可;

​ 之后我们可以枚举逆行的边,求逆行边的两个点到1号草场所在强联通分量的路即可,其路的权值即所经过强联通分量的全权值和;

​ 如何求最长路?正向建边反向建边跑SPFA最长路即可;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
#include<bits/stdc++.h>
#define maxn 100007
using namespace std;
int n,m,head[maxn],cent,dfn[maxn],low[maxn],stk[maxn],cnt,ans;
int col[maxn],tot,k,vis[maxn],num[maxn],dis1[maxn],dis2[maxn];
struct node{
	int next,to,from;
}edge[maxn<<3];

template<typename type_of_scan >
inline void scan(type_of_scan &x){
    x=0;char s=getchar();
    while(s<'0'||s>'9'){s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
}
template<typename tops,typename... Tops>
inline void scan(tops &x,Tops&... X){
    scan(x),scan(X...);
}
template<typename type_of_print>
inline void print(type_of_print x){
    if(x>9) print(x/10);
    putchar(x%10+'0');
}

inline void add(int u,int v){
	edge[++cent]=(node){head[u],v,u};head[u]=cent;
}

void Tarjan(int x){
	dfn[x]=++cnt,low[x]=cnt;
	stk[++k]=x;vis[x]=1;
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(!dfn[y]){
			Tarjan(y);
			low[x]=min(low[x],low[y]);
		}else if(vis[y]) low[x]=min(low[x],dfn[y]);//是vis[y]而不是vis[x] 
	}
	if(dfn[x]==low[x]){
		tot++;int z;
		do{
			z=stk[k--];
			col[z]=tot;
			vis[z]=0;
			num[tot]++;
		}while(z!=x);
	}
}

void spfa1(){
	memset(vis,0,sizeof(vis));
	queue<int >q;
	vis[col[1]]=1;dis1[col[1]]=num[col[1]];
	q.push(col[1]);
	while(!q.empty()){
		int x=q.front();q.pop();
		for(int i=head[x];i;i=edge[i].next){
			int y=edge[i].to;
			if(dis1[y]<dis1[x]+num[y]){
				dis1[y]=dis1[x]+num[y];
				if(!vis[y]) q.push(y),vis[y]=1;
			}
		}
		vis[x]=0;
	}
}

void spfa2(){
	memset(vis,0,sizeof(vis));
	queue<int >q;
	vis[col[1]]=1;dis2[col[1]]=num[col[1]];
	q.push(col[1]);
	while(!q.empty()){
		int x=q.front();q.pop();
		for(int i=head[x];i;i=edge[i].next){
			int y=edge[i].to;
			if(dis2[y]<dis2[x]+num[y]){
				dis2[y]=dis2[x]+num[y];
				if(!vis[y]) q.push(y),vis[y]=1;
			}
		}
		vis[x]=0;
	}
}

int main(){
//	freopen("cin.in","r",stdin);
//	freopen("cout.out","w",stdout);
	scan(n,m);
	for(int i=1,u,v;i<=m;i++)
		scan(u,v),add(u,v);
	for(int i=1;i<=n;i++)
		if(!col[i]) Tarjan(i);
	memset(head,0,sizeof head);cent=0;
	for(int i=1;i<=m;i++){
		int x=edge[i].from,y=edge[i].to;
		if(col[x]!=col[y]) add(col[x],col[y]);
	}
	spfa1();int ol=cent;
	memset(head,0,sizeof head);cent=0;
	for(int i=1;i<=ol;i++){
		int x=edge[i].from,y=edge[i].to;
		add(y,x);
	}
	spfa2();
	for(int i=1;i<=ol;i++){
		int x=edge[i].from,y=edge[i].to;
		if(dis1[x]&&dis2[y]) ans=max(ans,dis1[x]+dis2[y]);
		if(dis1[y]&&dis2[x]) ans=max(ans,dis1[y]+dis2[x]);
	}
	printf("%d\n",ans-num[col[1]]);
//	for(int i=1;i<=tot;i++) cout<<dis1[i]<<" "<<dis2[i]<<endl;
}

例题5

​ P2515 [HAOI2010]软件安装

​ Tarjan+树形背包;

​ 每次缩点,重新建图,然后跑个树形DP(蓝书上有);

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
#include<bits/stdc++.h>
#define maxn 107
using namespace std;
int n,m,head[maxn],val[maxn],cost[maxn],low[maxn],dfn[maxn],sz[maxn];
int col[maxn],cent,stk[maxn],tot,top,cnt,vis[maxn],w[maxn],in[maxn];
int f[maxn][maxn<<3],ans;
struct node{
	int next,from,to;
}edge[maxn<<4];

template<typename type_of_scan>
inline void scan(type_of_scan &x){
	type_of_scan f=1;x=0;char s=getchar();
	while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
	while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
	x*=f;
} 
template<typename top,typename... tops>
inline void scan(top &x,tops&... X){
	scan(x),scan(X...);
}

inline void add(int u,int v){
	edge[++cent]=(node){head[u],u,v};head[u]=cent;
}

void Tarjan(int x){
	dfn[x]=low[x]=++tot;vis[x]=1;
	stk[++top]=x;
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		if(!dfn[y]){
			Tarjan(y);
			low[x]=min(low[y],low[x]);
		}else if(vis[y]) low[x]=min(low[x],dfn[y]);
	}
	if(low[x]==dfn[x]){
		cnt++;int temp;
		do{
			temp=stk[top--];
			vis[temp]=0;
			col[temp]=cnt;
			sz[cnt]+=cost[temp];
			w[cnt]+=val[temp];
		}while(temp!=x);
	}
}

void dfs(int x){
	if(x) for(int t=m;t>=sz[x];t--) f[x][t]=w[x];
	for(int i=head[x];i;i=edge[i].next){
		int y=edge[i].to;
		dfs(y);
		for(int t=m-sz[x];t>=0;t--){
			for(int j=t;j>=0;j--)
				f[x][t+sz[x]]=max(f[x][t+sz[x]],f[x][t+sz[x]-j]+f[y][j]);
		}
	}
	return ;
}

int main(){
	scan(n,m);
	for(int i=1;i<=n;i++) scan(cost[i]);
	for(int i=1;i<=n;i++) scan(val[i]);
	for(int i=1,x;i<=n;i++) {
		scan(x);
		if(x) add(x,i);
	}
	for(int i=1;i<=n;i++) if(!dfn[i]) Tarjan(i);
	int lim=cent;cent=0;
	memset(head,0,sizeof head);
	for(int i=1;i<=lim;i++){
		int x=edge[i].from,y=edge[i].to;
		if(col[x]!=col[y]) add(col[x],col[y]),in[col[y]]++;
	}
	for(int i=1;i<=cnt;i++) if(!in[i]) add(0,i);
	dfs(0);
	for(int i=0;i<=m;i++) ans=max(ans,f[0][i]);
	printf("%d\n",ans);
}
/*
3 10
5 5 6
2 3 4
0 1 1
*/
TO BE CONTINUE
本站访问次数：