A Huster

0%

扫描线

Posted on Valine:

请在学习之前有一定的线段树基础

在一些题中，它总会给你一些矩形，之后让你求总覆盖面积。

它的难点在于，有重叠面积，如果只是罗列情况，那么只会一事无成。

所以说，这里就引进了扫描线做法；

其实它的原理很简单，只是底*高而已，只是分段求解；

而问题大概的图就是这样

alt

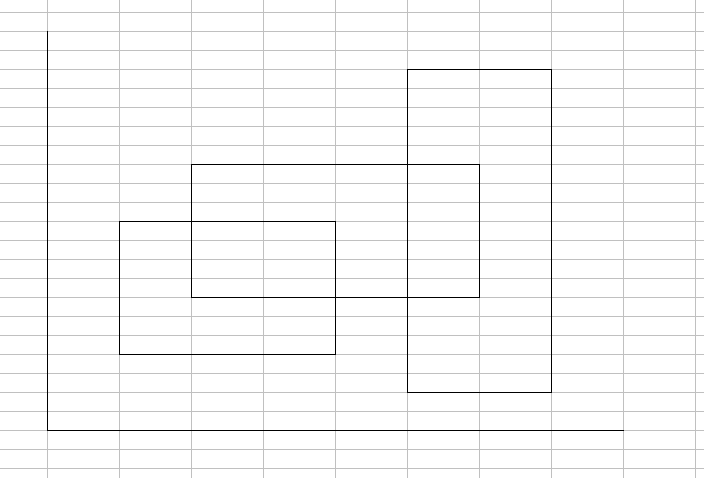
根据我刚刚说的分段求解和底*高，那么我们就可以推测出扫描线是什么了

它是由矩形的上边和下边构成，并记录其左右端点和其所在的纵坐标；

img

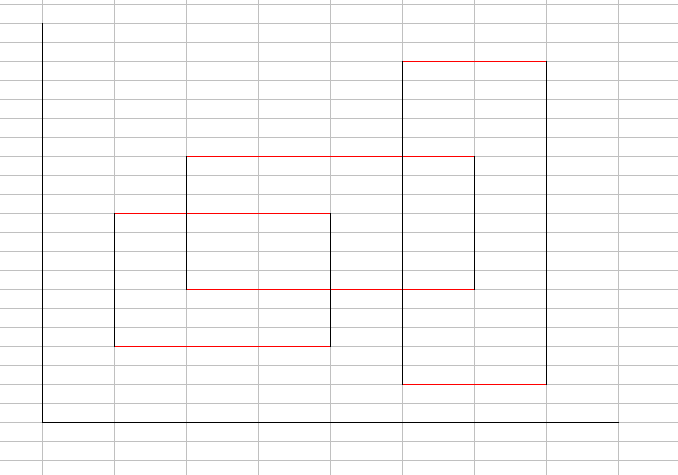
图中标红的即为扫描线，那么我们用它做什么？

根据 S=ah，那么我们可以将扫描线按*纵坐标排序，这样分步求解。

这是扫描线的储存

1
2
3
4
5
struct node{
    int x,y;//左右端点坐标 
    int h;//还是按 扫描线写，这个是y轴坐标 
    int d;//标记这个线是不是上界或下界 
}s[maxn<<3];//扫描线

那么便可以得到高，即

s[i+1].h-s[i].h

之后考虑存底，只需要用线段树维护即可；

当扫描线为下界时，应当将扫描线所在区域加入线段树，而当为上界时再减去即可；

由于底边过大，不可能全部建树，这里给出了离散化做法，还有动态开点做法之后将会提到

由于找不到最合适的模板题，只能拿这个来充数 P2061 [USACO07OPEN]城市的地平线City Horizon

1
2
3
4
5
6
7
8
9
10
11
12
13
14
　  scanf("%d",&n);
for(int i=1,a,b,h;i<=n;i++){
    scanf("%d%d%d",&a,&b,&h);
    ls[++cent]=a;//其实是用来离散化的 
    s[cent]=(node){a,b,0,1};
    ls[++cent]=b;
    s[cent]=(node){a,b,h,-1};
}
sort(ls+1,ls+1+cent);//离散化初始 
sort(s+1,s+1+cent);ls[++m]=ls[1];
for(int i=2;i<=cent;i++){
    if(ls[i]!=ls[i-1])
        ls[++m]=ls[i];//去重 
}

这便是简单的离散化，当然，你也可以排序后用unique函数，得到m和ls数组，这个可以网上查询，这里便不再赘述

之后是线段树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void push_up(int l,int r,int p){
    if(mark[p]) tree[p].sum=ls[r]-ls[l];//如何避免少减？ 
    else if(l==r) tree[p].sum=0;
    else tree[p].sum=tree[le(p)].sum+tree[re(p)].sum;
}

void up_date(int p,int d,int L,int R){
    int l=tree[p].l,r=tree[p].r;
    if(l>=L&&r<=R){
        mark[p]+=d;
        push_up(l,r,p);
        return ;
    }
    if(r-1==l) return ;
    int mid=l+r>>1;
    if(mid>=L) up_date(le(p),d,L,R);
    if(mid<R) up_date(re(p),d,L,R);
    push_up(l,r,p);
}

这里的代码是我根据多种方面得出，但是仍由问题，即代码所说的，因为在线段数中 l 是可以等于 r 的，但是线段的长度必须由两个不同的数得出，这是不行的

所以，我们可以先建出一颗空树

1
2
3
4
5
6
7
8
9
void build(int l,int r,int p){
    tree[p].l=l;
    tree[p].r=r;
    tree[p].sum=0;
    if(l==r-1) return ;
    int mid=l+r>>1;
    build(l,mid,le(p)),build(mid,r,re(p));/*注意，mid在左子树和右子树中都有出现，所以在 
    叶子节点，r=l+1，这个也是对return 的解释*/ 
}

所以说，这样便避免了这个问题，不过请读者注意这些点，这些便是易错的小细节

1
2
3
4
5
6
7
build(1,m,1);
for(int i=1;i<=cent;i++){
    int l=search(s[i].x,ls);//二分寻找离散化位置
    int r=search(s[i].y,ls);
    up_date(1,s[i].d,l,r);// 用线段树更新sum，即矩形底边 
    rt+=(ll)tree[1].sum*1ll*(s[i+1].h-s[i].h);
}

这里是主函数的计算，而search有解释，也可以用lower_bound，推荐提前处理出来，否则可能会提高时间复杂度，这不是我们所期望的

这样的做法不易错是真的，这里给出二分search做法

1
2
3
4
5
6
7
8
9
int search(int pur,int* x){
    int l=1,r=m;
    while(l<r){
        int mid=l+r>>1;
        if(x[mid]<pur) l=mid+1;
        else r=mid;
    }
    return l;
}

这便是整个过程，这里给出code

Code

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<bits/stdc++.h>
#define ll long long
#define maxn 40007
#define le(x) x<<1
#define re(x) x<<1|1
using namespace std;
int n,cent,m,mark[maxn<<4];
int ls[maxn<<3];
ll rt;
struct tr{
    ll sum;
    int l,r;
}tree[maxn<<4];
struct node{
    int x,y;//左右端点坐标 
    int h;//还是按 扫描线写，这个是y轴坐标 
    int d;//标记这个线是不是上界或下界 
}s[maxn<<3];//扫描线 

bool operator <(node a,node b){
    return a.h<b.h;
}

void push_up(int l,int r,int p){
    if(mark[p]) tree[p].sum=ls[r]-ls[l];//如何避免少减？ 
    else if(l==r) tree[p].sum=0;
    else tree[p].sum=tree[le(p)].sum+tree[re(p)].sum;
}

void up_date(int p,int d,int L,int R){
    int l=tree[p].l,r=tree[p].r;
    if(l>=L&&r<=R){
        mark[p]+=d;
        push_up(l,r,p);
        return ;
    }
    if(r-1==l) return ;
    int mid=l+r>>1;
    if(mid>=L) up_date(le(p),d,L,R);
    if(mid<R) up_date(re(p),d,L,R);
    push_up(l,r,p);
}

void build(int l,int r,int p){
    tree[p].l=l;
    tree[p].r=r;
    tree[p].sum=0;
    if(l==r-1) return ;
    int mid=l+r>>1;
    build(l,mid,le(p)),build(mid,r,re(p));/*注意，mid在左子树和右子树中都有出现，所以在 
    叶子节点，r=l+1，这个也是对return 的解释*/ 
}

int search(int pur,int* x){
    int l=1,r=m;
    while(l<r){
        int mid=l+r>>1;
        if(x[mid]<pur) l=mid+1;
        else r=mid;
    }
    return l;
}

int main(){
//    freopen("cin.in","r",stdin);
    scanf("%d",&n);
    for(int i=1,a,b,h;i<=n;i++){
        scanf("%d%d%d",&a,&b,&h);
        ls[++cent]=a;//其实是用来离散化的 
        s[cent]=(node){a,b,0,1};
        ls[++cent]=b;
        s[cent]=(node){a,b,h,-1};
    }
    sort(ls+1,ls+1+cent);//离散化初始 
    sort(s+1,s+1+cent);ls[++m]=ls[1];
    for(int i=2;i<=cent;i++){
        if(ls[i]!=ls[i-1])
            ls[++m]=ls[i];//去重 
    }
    build(1,m,1);
    for(int i=1;i<=cent;i++){
        int l=search(s[i].x,ls);//二分寻找离散化位置
        int r=search(s[i].y,ls);
        up_date(1,s[i].d,l,r);// 用线段树更新sum，即矩形底边 
        rt+=(ll)tree[1].sum*1ll*(s[i+1].h-s[i].h);
    }
    cout<<rt<<endl;
    return 0;
}

7.24 补充：

LUOGU P1502 窗口的星星

　　

题目背景

小卡买到了一套新房子，他十分的高兴，在房间里转来转去。

题目描述

晚上，小卡从阳台望出去，“哇~~~~好多星星啊”，但他还没给其他房间设一个窗户，天真的小卡总是希望能够在晚上能看到最多最亮的星星，但是窗子的大小是固定的，边也必须和地面平行。这时小卡使用了超能力（透视术）知道了墙后面每个星星的位置和亮度，但是小卡发动超能力后就很疲劳，只好拜托你告诉他最多能够有总和多亮的星星能出现在窗口上。

输入输出格式

输入格式：

本题有多组数据，第一行为T 表示有T组数据T<=10

对于每组数据

第一行3个整数n，W，H，（n<=10000,1<=W,H<=1000000）表示有n颗星星，窗口宽为W，高为H。

接下来n行，每行三个整数xi，yi，li 表示星星的坐标在（xi，yi），亮度为li。（0<=xi,yi<2^31)

输出格式：

T个整数，表示每组数据中窗口星星亮度总和的最大值。

这道题的一个关键点是，将星星作为一个窗户的左下角（其实是为了不出现负数），将每一个星星都创一个窗户，之后寻找重叠部分

解释

alt

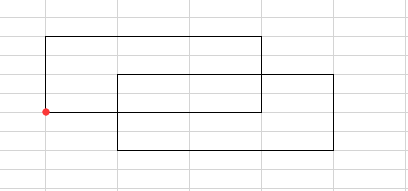
看这个图，这是两个相交的情况，矩形左下角是星星，然后如果有重叠部分，那么我们要贴着相交部分的上边和右边建一个窗户，那么就可以盖住这两个星星，

alt

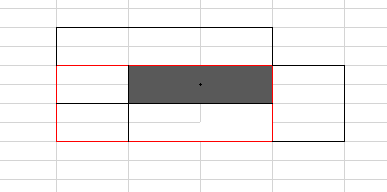
类比到所有星星是一样的，我们只要将矩形附上权值即可，用扫描线寻找。

但是这个边框不是不能包含星星吗？所以我们需要处理一些小细节，将矩形右边的横坐标减去1，也就是提前减去，再将扫描线上端-1，这就处理了边界问题；

并且在sort的时候当横坐标相同时，将加上的排在前面。

这个细节请一定要理解，否则wa了也不好调（因为不给数据），代码我会做上标记。

矩形权值直接附在扫描线上即可；

上一道例题中，我用离散化解决了范围大的问题，这里我们介绍动态开点做法；

首先不需要在意太多的离散化细节是一个优点，干干的介绍不是非常简洁，所以我直接附上代码讲解：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
#include<bits/stdc++.h>
#define maxn 10007
using namespace std;
int t,n,w,h,cnt,lim,root;
struct node{
    int x,l,r,w,d;
}a[maxn<<3];//扫描线 
struct tree{
    int le,ri,w,tag;
}tr[5000007];//动态开点的不同，le和ri记录的是左端点和右端点的p值 
//tr记住稍微大一点 （别 MLE 了 ），反正不会错 
template<typename type_of_scan>
inline void scan(type_of_scan &x){
    type_of_scan f=1;x=0;char s=getchar();
    while(s<'0'||s>'9') f=s=='-'?-1:1,s=getchar();
    while(s>='0'&&s<='9') x=(x<<3)+(x<<1)+s-'0',s=getchar();
    x*=f;
}

bool operator <(node x,node y){
    return x.x==y.x?x.d>y.d:x.x<y.x;
}//sort的细节*** 

inline void push_down(int p,int k){
    if(!tr[p].le) tr[p].le=++cnt;//没点开点 
    if(!tr[p].ri) tr[p].ri=++cnt;
    tr[tr[p].le].w+=k,tr[tr[p].ri].w+=k;
    tr[tr[p].le].tag+=k,tr[tr[p].ri].tag+=k;
}

void add(int nl,int nr,int l,int r,int &p,int k){
    if(!p) p=++cnt;//没点开点 
    if(nl<=l&&nr>=r){
        tr[p].w+=k,tr[p].tag+=k;
        return ;
    }
    if(tr[p].tag) push_down(p,tr[p].tag);tr[p].tag=0;
    int mid=(l+r)>>1;
    if(nl<=mid) add(nl,nr,l,mid,tr[p].le,k);
    if(nr>mid) add(nl,nr,mid+1,r,tr[p].ri,k);
    tr[p].w=max(tr[tr[p].le].w,tr[tr[p].ri].w);
}//与线段树相同 

inline void work(){
    int ans=0;memset(tr,0,sizeof tr);
    scan(n);scan(w),scan(h);
    for(int i=1,x,y,v;i<=n;i++)
        scan(x),scan(y),scan(v),lim=max(x+w+1,lim),//lim是线段树范围 
        a[(i<<1)-1]=(node){x,y,y+h-1,v,1},//强行转换格式，-1的细节** 
        a[i<<1]=(node){x+w-1,y,y+h-1,v,-1};//细节** 
    sort(a+1,a+1+2*n);//细节** 
    for(int i=1;i<=2*n;i++){
        add(a[i].l,a[i].r,1,lim,root,a[i].w*a[i].d);
        ans=max(ans,tr[root].w);//直接用整棵树更新就好啦 
    }
    printf("%d\n",ans);
}

int main(){
    scan(t);
    while(t--) work();
    return 0;
}

扫描线2种方法都已经讲完，可以再找一些题练习一下；

本站访问次数：