莫队思想浅谈

莫队，基于分块思想。

所以说，在学习莫队时可以先了解一下分块的优化原理，这对于莫队的理解会有帮助；

我们将分层次讲解，难度不断增加，并附有例题。。。（由于博主太烂懒，所以莫队的模板概念知识只会在这里叙述）

1.莫队：

　　基础的莫队是用来解决区间离线查询问题，利用分块原理和排序，将查询时的重叠部分集中以来优化的算法，大多的算法的复杂度为$O(nsqrt(n))$，实际更优；

　　莫队代码一般很短，且有套路可言，所以应熟练掌握；

　　表述完毕，开始讲解：

　　P1972 [SDOI2009]HH的项链

题目描述

HH 有一串由各种漂亮的贝壳组成的项链。HH 相信不同的贝壳会带来好运，所以每次散步完后，他都会随意取出一段贝壳，思考它们所表达的含义。HH 不断地收集新的贝壳，因此，他的项链变得越来越长。有一天，他突然提出了一个问题：某一段贝壳中，包含了多少种不同的贝壳？这个问题很难回答……因为项链实在是太长了。于是，他只好求助睿智的你，来解决这个问题。

输入格式

第一行：一个整数N，表示项链的长度。

第二行：N 个整数，表示依次表示项链中贝壳的编号（编号为0 到1000000 之间的整数）。

第三行：一个整数M，表示HH 询问的个数。

接下来M 行：每行两个整数，L 和R（1 ≤ L ≤ R ≤ N），表示询问的区间。

输出格式

M 行，每行一个整数，依次表示询问对应的答案。

　　莫队的一道例题，但是这道题很恶心，数据专门卡了莫队，不过不用担心，我们可以吸口氧，再吸口臭氧，然后再有一些优化就可以A掉（如果实在过不了，后面附上了树状数组代码），然后让我们来讲解；

设第一个查询的区间为[ l1,r1 ] , 第二个查询的区间为[ l2,r2 ]；

既然已经说莫队时暴力结构，那么就能猜到它的统计方式是暴力统计；

引入两个指针 l ，r，首先让 l 移动，让l = l1，移动时进行增加或减去操作，像这道题，是颜色个数的减少或增加，那么暴力统计就可以不说了吧；

在移动到第二个区间时，用同样的操作移动；

但是这个不就是纯暴力了吗，不知道你是否有这样的疑问；

但是当我们将区间分块，再将区间按l，r所在块进行排序，那么每次移动的时间复杂度就变成了sqrt（n）（因为我们分成了sqrt（n）个块）；

这样就应该明白其原理，如果真的还是不懂了话，那么可以看看代码；

Code（带有O2优化，O3优化和排序优化）

// luogu-judger-enable-o2
//luogu的O2，NOIP没有 
#pragma GCC optimize(3)//O3优化，联赛时没有 
#include<bits/stdc++.h>
#define maxn 500007
#define Ri register int//指针优化 
using namespace std;
int n,m,be[maxn],a[maxn],unit,col[maxn*10],ans,l=1,r,prin[maxn];
struct query{int l,r,id;}q[maxn];//query的结构体，便于排序 
inline bool cmp(query a,query b){
    return be[a.l]^be[b.l]?be[a.l]<be[b.l]:(be[a.l]&1)?a.r<b.r:a.r>b.r;
}//排序小优化 
inline void syst(int x,int d){col[x]+=d;if(d>0)ans+=(col[x]==1);if(d<0)ans-=(col[x]==0);}
//d==1为增加，d==-1为减少 
template<typename type_of_scan>
inline void scan(type_of_scan &x){
    type_of_scan f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}
template<typename Tops,typename... tops>
inline void scan(Tops &x,tops&... X){
    scan(x),scan(X...);
}
template<typename type_of_print>
inline void print(type_of_print x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) print(x/10);
    putchar(x%10+'0');
} 

int main(){
    scan(n);unit=sqrt(n);
    for(Ri i=1;i<=n;i++)
        scan(a[i]),be[i]=i/unit+1;//分块 
    scan(m);
    for(Ri i=1;i<=m;i++)
        scan(q[i].l,q[i].r),q[i].id=i;
    sort(q+1,q+1+m,cmp);//排序 
    for(Ri i=1;i<=m;i++){
        while(l<q[i].l) syst(a[l],-1),l++;//减去l上这个数 
        while(l>q[i].l) syst(a[l-1],1),l--;//加上l-1上这个数 
        while(r<q[i].r) syst(a[r+1],1),r++; 
        while(r>q[i].r) syst(a[r],-1),r--;
        prin[q[i].id]=ans;//记录答案 
    }
    for(Ri i=1;i<=m;i++)
        print(prin[i]),putchar('\n');
}

这个代码至少过了这道题，但是仍然很悬，所以尽可能地优化常数

附上树状数组代码

#include<bits/stdc++.h>
#define maxn 500007
using namespace std;
int n,m,tree[maxn<<2],a[maxn],cent,col[maxn*10],pre[maxn*10];
struct query{int l,r,id,ans;}q[maxn];
inline bool cmp(query a,query b){return a.r==b.r?a.l<b.l:a.r<b.r;}
inline bool cmp1(query a,query b){return a.id<b.id;}
inline int lowbit(int x){return x&-x;}
inline void add(int x,int d){for(;x<=n;x+=lowbit(x)) tree[x]+=d;}
inline int ask(int x){int ans=0;while(x) ans+=tree[x],x-=lowbit(x);return ans;}

template<typename type_of_scan>
inline void scan(type_of_scan &x){
    type_of_scan f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}
template<typename Tops,typename... tops>
inline void scan(Tops &x,tops&... X){
    scan(x),scan(X...);
}
template<typename type_of_print>
inline void print(type_of_print x){
    if(x<0) putchar('-'),x=-x;
    if(x>9) print(x/10);
    putchar(x%10+'0');
}

int main(){
    scan(n);
    for(int i=1;i<=n;i++)
        scan(a[i]);
    scan(m);
    for(int i=1;i<=m;i++)
        scan(q[i].l,q[i].r),q[i].id=i;
    sort(q+1,q+1+m,cmp);
    for(int i=1;i<=m;i++){
        while(cent<q[i].r){
            add(++cent,1);
            col[a[cent]]++;
            if(col[a[cent]]>1){
                add(pre[a[cent]],-1);
                pre[a[cent]]=cent;
                col[a[cent]]--;
            }else pre[a[cent]]=cent;
        }
        q[i].ans=ask(q[i].r)-ask(q[i].l-1);
    }
    sort(q+1,q+1+m,cmp1);
    for(int i=1;i<=m;i++)
        print(q[i].ans),putchar('\n');
    return 0;
}

这样应该可以去水题了，紫题，不用谢我；

2.带修莫队：

例题：P1903 [国家集训队]数颜色 / 维护队列

题目描述

墨墨购买了一套N支彩色画笔（其中有些颜色可能相同），摆成一排，你需要回答墨墨的提问。墨墨会向你发布如下指令：

1、 Q L R代表询问你从第L支画笔到第R支画笔中共有几种不同颜色的画笔。

2、 R P Col 把第P支画笔替换为颜色Col。

为了满足墨墨的要求，你知道你需要干什么了吗？

输入格式

第1行两个整数N，M，分别代表初始画笔的数量以及墨墨会做的事情的个数。

第2行N个整数，分别代表初始画笔排中第i支画笔的颜色。

第3行到第2+M行，每行分别代表墨墨会做的一件事情，格式见题干部分。

输出格式

对于每一个Query的询问，你需要在对应的行中给出一个数字，代表第L支画笔到第R支画笔中共有几种不同颜色的画笔。

　　带修莫队其实没什么，只要查询是离线就别虚，只要加入一个时间指针t即可。

　　但是如果只是单纯的分块了话，可能时间会超，我们看一下分块块数unit，

　　当同l块时，移动需要nunit，当l块之间r携带移动时需要(n^2)/unit，当时间 t 移动时仍然有 l 和 r 块的移动，所以需要 (n^2t)/(unit^2)

　　时间复杂度时三个移动取最大值（因为省略常数），发现如果unit取sqrt（n）时，最坏时间复杂度为n^2，这不是我们所期望的，

　　将t看似为n那么整理第三个为(n^3)/(unit^2)，那么让两两相等，三种情况取最优，发现当unit=n^(2/3)时，时间复杂度最优，为O(n^(5/3))；

　　那么就可以看代码了。。。

#include<bits/stdc++.h>
#define maxn 50007
#define Ri register int
using namespace std;
int n,m,col[maxn*100],s[maxn],unit,be[maxn],T,l=1,r;
int cent,t,ans[maxn],Ans,now[maxn];
struct query{
    int l,r,Time,id;
}q[maxn];//查询数组 
struct change{
    int exfo,New,Old;
}c[maxn];//change数组 

template<typename type_of_scan>
inline void scan(type_of_scan &x){
    type_of_scan f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}
bool cmp(query a,query b){
    if(be[a.l]!=be[b.l]) return a.l<b.l;
    else if(be[a.r]!=be[b.r]) return a.r<b.r;
    return a.Time<b.Time;
}//不同的排序方式 

inline void syst(int x,int d){col[x]+=d;if(d>0)Ans+=(col[x]==1);if(d<0)Ans-=(col[x]==0);}
inline void spe(int x,int d){if(l<=x&&x<=r) syst(d,1),syst(s[x],-1);s[x]=d;}//t指针移动方式 

int main(){
    scan(n),scan(m);unit=pow(n,0.666666);//2/3=0.6666666，6越多越精确 
    for(int i=1;i<=n;i++)
        scan(s[i]),now[i]=s[i],be[i]=i/unit+1;
    for(int i=1,x,y;i<=m;i++){
        char type;
        scanf(" %c %d%d",&type,&x,&y);
        if(type=='Q') q[++cent]=(query){x,y,t,cent};
        else if(type=='R') c[++t]=(change){x,y,now[x]},now[x]=y;
    }
    sort(q+1,q+1+cent,cmp);
    for(int i=1;i<=cent;i++){    
        while(T<q[i].Time) spe(c[T+1].exfo,c[T+1].New),T++;
        while(T>q[i].Time) spe(c[T].exfo,c[T].Old),T--;
        while(l<q[i].l) syst(s[l],-1),l++;
        while(l>q[i].l) syst(s[l-1],1),l--;
        while(r<q[i].r) syst(s[r+1],1),r++;
        while(r>q[i].r) syst(s[r],-1),r--;
        ans[q[i].id]=Ans;
    }
    for(int i=1;i<=cent;i++)
        printf("%d\n",ans[i]);
}

3.树上莫队：

要说树上操作，那么莫队可以操作的有两种类型，第一种是子树统计，第二种是路径统计，那么让我们详细来看；

警告：前方有dfs序和euler序出现；

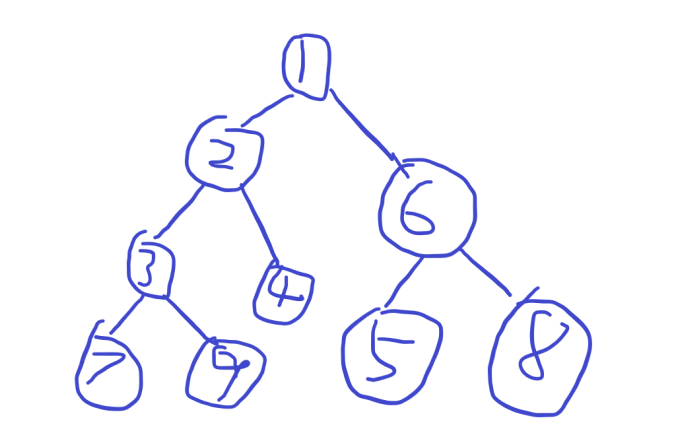
1.子树统计

　　这个如果只是一颗子树单纯的统计非常简单，只要一次dfs求出dfs序和子树size即可，你会发现子树上的dfs序时连续的，直接查询一段区间即可；

　　有点丑，不要介意，它的dfs序是1 2 3 7 9 4 6 5 8

　　　　2的子树序列即为 2 3 7 9；

　　这个应该不需要再解释了吧。。。

　　但是在两颗子树上统计再加上换根操作是不是很毒瘤，我们在后面会讲到；

2.路径统计

　　莫队只能维护序列，所以我们将子树转化为dfs序，将其从树中拿出，维护其序列，那么路径上怎么办呢

　　　　我们再拿出这个图（我知道很丑！）

　　　　不知道euler序？没关系，我解释就行了，euler序将一个数记录两遍，进的时候记录一遍，出的时候记录一遍；

　　　　我们将序列列出来就很清晰了： 1 2 3 7 7 9 9 3 4 4 2 6 5 5 8 8 6 1;

　　　　那么每个数字都出现了两遍，我们设节点 i 在euler序中第一次出现的位置为first [ i ] ，第二次出现的位置为last [ i ] 。

　　　　观察路径2->9，你会发现路径上first [ 2 ] -> fisrt [ 9 ]：2 3 7 7 9，其中路径上的点都只出现了一次，出现两次的都不在路径上，证明也很简单，这里就不再赘述。

　　　　当然last [ 2 ] -> last [ 9 ]是一样的，只是顺序不一样。

　　　　但是这个只是一种情况——当两个点中有一个点是另一个点子树的一部分，或者问题转换一下一个点是另一个点的LCA，如刚刚的2是9的LCA。

　　　　但是当不在同一颗子树上会发生什么？

　　　　例如3 -> 6：3 7 7 9 9 3 4 4 2 6 5 5 8 8 6，这是3和6出现两次时序列，我们已经发现没有1这个点，我们选取last [ 3 ] -> first [ 6 ] : 3 4 4 2 6，其中路径上的点3 2 6都出现

　　　　但是1却没有出现，我们可以发现1时LCA（3，6），所以euler序中在这种情况下是没有LCA的，那么我们在统计答案时将其加上，然后再减去。

　　　　两种情况都已经讨论完毕，我们只要在存q数组时做个lca的标记即可。

　　　　这里给出一道　　例题　　

题目描述

给定一个n个节点的树，每个节点表示一个整数，问u到v的路径上有多少个不同的整数。

输入格式

第一行有两个整数n和m（n＝40000，m＝100000）。

第二行有n个整数。第i个整数表示第i个节点表示的整数。

在接下来的n-1行中，每行包含两个整数u v，描述一条边（u，v）。

在接下来的m行中，每一行包含两个整数u v，询问u到v的路径上有多少个不同的整数。

输出格式

对于每个询问，输出结果。

　　　　这是模板测试，只需要分类讨论，直接套莫队；

#include<bits/stdc++.h>
#define maxn 40007
#define N 100007
using namespace std;
int n,m,ls[maxn],euler[maxn<<1],ans[N],cent,cnt,dep[maxn<<1],num[maxn<<1],l=1,r,now;
int first[maxn<<1],last[maxn<<1],b[maxn],fa[maxn<<1][30],be[maxn<<1],vis[maxn<<1];
int head[maxn<<1],unit,col[maxn];
struct query{
    int l,r,id,lca;
}q[N];
struct node{
    int next,to;
}edge[N<<2];
inline void add(int u,int v){
    edge[++cent]=(node){head[u],v};head[u]=cent;
    edge[++cent]=(node){head[v],u};head[v]=cent;
}

void dfs(int x){
    euler[++cnt]=x;first[x]=cnt;
    for(int i=head[x];i;i=edge[i].next){
        int y=edge[i].to;
        if(fa[x][0]==y) continue;
        dep[y]+=dep[x]+1;fa[y][0]=x;
        dfs(y);
    }
    euler[++cnt]=x;last[x]=cnt;
}//在完成LCA初始化的同时完成euler序的记录 

void init(){
    dep[1]=1,fa[1][0]=-1;dfs(1);
    for(int i=1;i<=25;i++){
        for(int k=1;k<=n;k++){
            if(fa[k][i-1]<0) fa[k][i]=-1;
            else fa[k][i]=fa[fa[k][i-1]][i-1];
        }
    }
}

int getlca(int x,int y){
    if(dep[x]<dep[y]) swap(x,y);
    for(int i=0,d=dep[x]-dep[y];d;d>>=1,i++)
        if(d&1) x=fa[x][i];
    if(x==y) return x;
    for(int i=25;i>=0;i--)
        if(fa[x][i]!=fa[y][i]){
            x=fa[x][i];
            y=fa[y][i];
        }
    return fa[x][0];
}
//这里是倍增求LCA，当然也可以2遍dfs+树剖 

inline bool cmp(query a,query b){
    return be[a.l]^be[b.l]?be[a.l]<be[b.l]:(be[a.l]&1?a.r<b.r:a.r>b.r); 
}//排序小优化

inline void syst(int x){
    vis[x] ? now -= (!--num[ls[x]]):now += !num[ls[x]]++;
    //CASE 1 ：前者减去，而！是为了判断是否应该减取（true=1，false=0） 
    //CASE 2 ：后者加上，！同上面所说 
    vis[x] ^= 1;//异或操作可以方便的转换出现次数 
}

int main(){
    scanf("%d%d",&n,&m);unit=sqrt(2*n);//记住euler序是2*n 
    for(int i=1;i<=n;i++)
        scanf("%d",&ls[i]),b[i]=ls[i];
    sort(b+1,b+1+n);
    int tot=unique(b+1,b+1+n)-b-1;
    for(int i=1;i<=n;i++)
        ls[i]=lower_bound(b+1,b+1+tot,ls[i])-b;
    //由于数值太大，我们进行离散化 
    for(int i=1,a,b;i<=n-1;i++)
        scanf("%d%d",&a,&b),add(a,b);
    init();//初始化 
    for(int i=1;i<=cnt;i++) be[i]=i/unit+1;//分块 
    for(int i=1,L,R;i<=m;i++){
        scanf("%d%d",&L,&R);
        int lca=getlca(L,R);q[i].id=i;
        if(first[L]>first[R]) swap(L,R);//小的在前面哦 
        if(lca==L){//CASE 1 ： 
            q[i].l=first[L];
            q[i].r=first[R];
            q[i].lca=0;//不需要考虑LCA 
        }else {//CASE 2 ： 
            q[i].l=last[L];
            q[i].r=first[R];
            q[i].lca=lca;
        }
    }
    sort(q+1,q+1+m,cmp);
    for(int i=1;i<=m;i++){
        int lca=q[i].lca;
        while(l<q[i].l) syst(euler[l]),l++;
        while(l>q[i].l) syst(euler[l-1]),l--;
        while(r<q[i].r) syst(euler[r+1]),r++;
        while(r>q[i].r) syst(euler[r]),r--;
        if(lca) syst(lca);//判断是否需要考虑LCA 
        ans[q[i].id]=now;
        if(lca) syst(lca);
    }
    for(int i=1;i<=m;i++)
        printf("%d\n",ans[i]);
    return 0;
}

如果您已经AC了这几道题，恭喜您已经大概掌握莫队的框架。（这几道题不是小意思嘛，博主太菜了）

由于博主太菜，还没有学回滚莫队，所以这里先不再说（逃ε=ε=ε=┏(゜ロ゜;)┛）

不过这里再留下一道模板题，糖果公园——带修树上莫队，两种算法相结合，不要虚，虽然是黑题

这里不再附上代码，请原谅。。。

拓展提升

4.双指针莫队

　　其实这才是莫队的本质，虽然带修莫队是三指针，但是别忘了其时间复杂度还是很难让人接受的（尤其是常数巨大的博主），所以我们还是用双指针的比较多。

　　我们以上看到的莫队是一个区间的查询，一个指针维护l，一个指针维护r，然后再用分块排序；

　　但是当我们遇见了两个区间怎么办？比如说这道题P5268 [SNOI2017]一个简单的询问，请读者不要被其吓住，这其实只有一个普通莫队的难度，只是需要从原来的思维跳出来

　　真正理解莫队双指针的作用。

　　设该函数为f( l1 , r1 , l2 , r2)，那么可以拆成f（ 1 , l1-1 , 1 , l2-1 ) + f ( 1 , r1, 1 , r2 ) - f (1 , l1-1 , 1 , r2) - f ( 1 , l2 - 1 , 1 , r2 )；

　　这里用到了容斥原理，将区间容斥，那么我们就可以引用莫队，维护两个变量，双指针移动，分块排序（博主太唠叨了）

　　这里附上代码：

#include<bits/stdc++.h>
#define maxn 500007
using namespace std;
int n,m,a[maxn],be[maxn],unit,ans[maxn],ol,all;
int t[maxn][2];
struct node{
    int l,r,d,id;
}q[maxn<<3];

template<typename type_of_scan>
inline void scan(type_of_scan &x){
    type_of_scan f=1;x=0;char s=getchar();
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    x*=f;
}

bool cmp(node a,node b){
    return be[a.l]==be[b.l]?a.r<b.r:be[a.l]<be[b.l];
}

inline void add(int x,int type){
    ol+=t[a[x]][type^1];
    t[a[x]][type]++;
} 
inline void del(int x,int type){
    ol-=t[a[x]][type^1];
    t[a[x]][type]--;
}//简单的操作 

int main(){
    scan(n);unit=sqrt(n)+1;
    for(int i=1;i<=n;i++) scan(a[i]),be[i]=(i-1)/unit+1;
    scan(m);
    for(int i=1,l1,r1,l2,r2;i<=m;i++){
        scan(l1),scan(r1),scan(l2),scan(r2);
        q[++all].l=r1,q[all].r=r2,q[all].d=1,q[all].id=i;
        q[++all].l=l2-1,q[all].r=r1,q[all].d=-1,q[all].id=i;
        q[++all].l=l1-1,q[all].r=r2,q[all].d=-1,q[all].id=i;
        q[++all].l=l1-1,q[all].r=l2-1,q[all].d=1,q[all].id=i;
    }//拆成四个询问 ，id一样 
    sort(q+1,q+1+all,cmp);//排序是一样的 
    int l=0,r=0;
    for(int i=1;i<=all;i++){
        while(l<q[i].l) add(++l,0);
        while(l>q[i].l) del(l--,0);//两个指针要分开标记用1和0即可（可以异或） 
        while(r<q[i].r) add(++r,1);
        while(r>q[i].r) del(r--,1);
        ans[q[i].id]+=ol*q[i].d;// 4个询问最后会累加在一起 
    }
    for(int i=1;i<=m;i++) printf("%d\n",ans[i]);
}